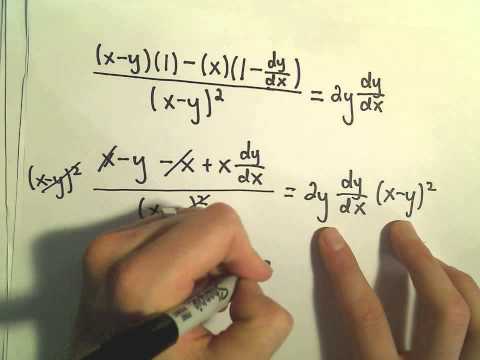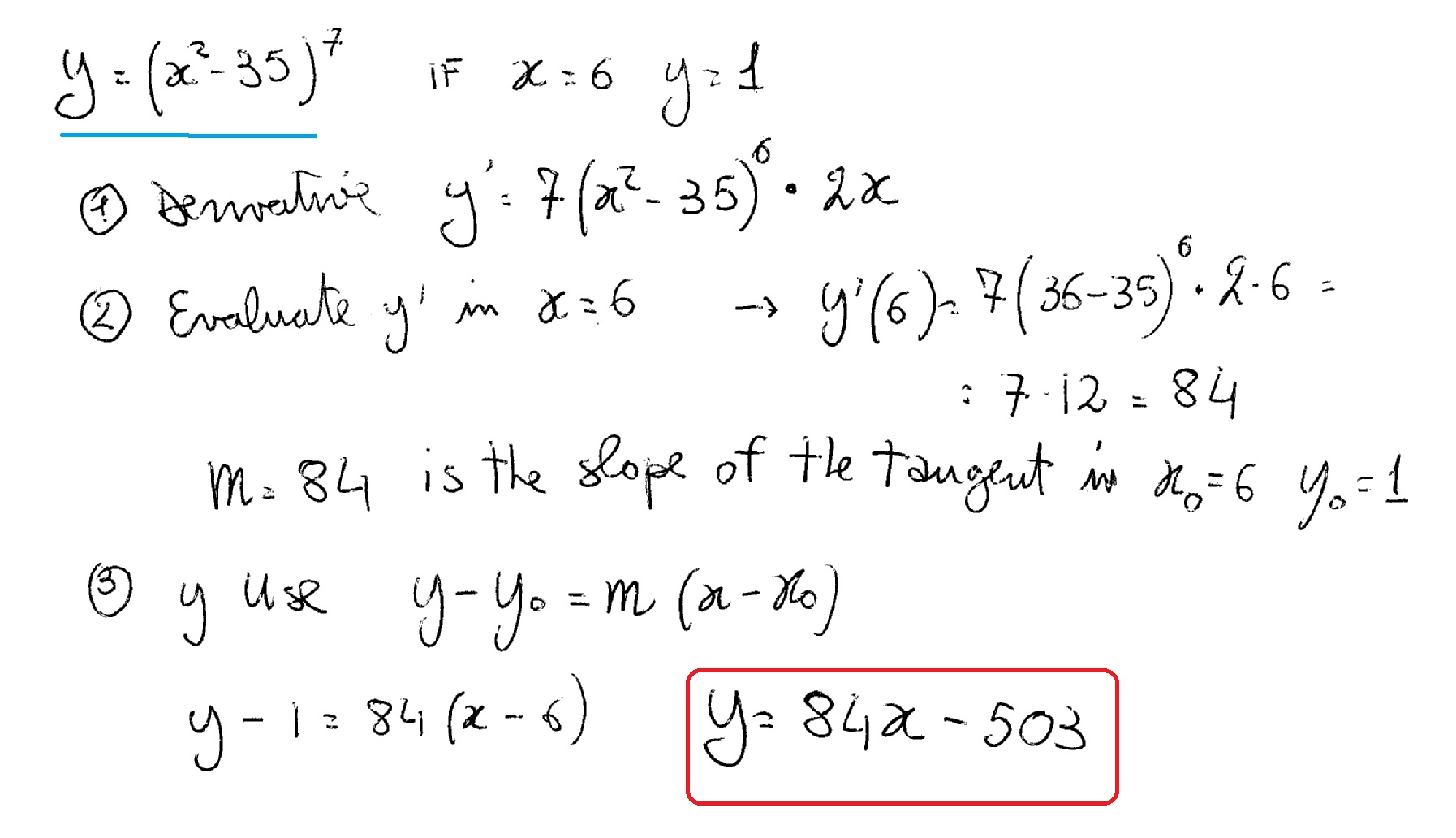We have already studied how to find equations of tangent lines to functions and the rate of change of a function at a specific point. In all these cases we had the explicit equation for the function and differentiated these functions explicitly. Suppose instead that we want to determine the equation of a tangent line to an arbitrary curve or the rate of change of an arbitrary curve at a point.
In this section, we solve these problems by finding the derivatives of functions that define implicitly in terms of . In this section, we solve these problems by finding the derivatives of functions that define \(y\) implicitly in terms of \(x\). A horizontal tangent line is a mathematical feature on a graph, located where a function's derivative is zero. This is because, by definition, the derivative gives the slope of the tangent line. Horizontal lines have a slope of zero.
Therefore, when the derivative is zero, the tangent line is horizontal. To find horizontal tangent lines, use the derivative of the function to locate the zeros and plug them back into the original equation. Horizontal tangent lines are important in calculus because they indicate local maximum or minimum points in the original function.
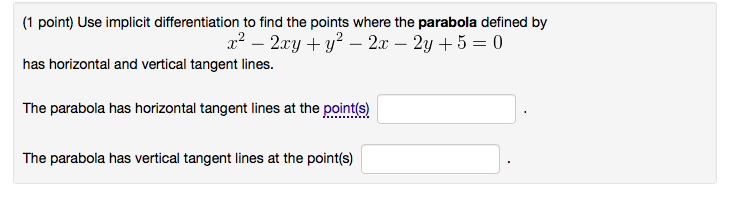
Dy/dx is the slope of the tangent line. In this problem the differentiation has already been done, in "implicit" form - that is, both x and y occur in the function. Set the numerator to zero to find where the slope is horizontal, and set the denominator to zero to find vertical tangents. Knowing only the derivative, you will not be able to specify the actual point - just one of its two coordinates.
If we want to find the slope of the line tangent to the graph of at the point , we could evaluate the derivative of the function at . On the other hand, if we want the slope of the tangent line at the point , we could use the derivative of . However, it is not always easy to solve for a function defined implicitly by an equation. The process of finding using implicit differentiation is described in the following problem-solving strategy.
Need to see a bunch of random derivative problems? Has it been a while since you took Calculus 1 and you have forgotten some of your formulas? The graph of z1 shown in Lesson 13.1 suggests that one branch of the curve has a horizontal tangent at and another branch has a vertical tangent at . The formula for dy/dx takes the form 0/0 at . Determine the \(x\)-\(y\) coordinates of the points where the following parametric equations will have horizontal or vertical tangents.
The next topic that we need to discuss in this section is that of horizontal and vertical tangents. We can easily identify where these will occur (or at least the \(t\)'s that will give them) by looking at the derivative formula. Using implicit differentiation find y', so that you have a formula for slopes of tangent lines to the graph of the original function.
Using implicit differentiation we can treat relations which are not quite functions like they were functions. In particular, we can find the slopes of lines tangent to curves which are not graphs of functions. Quite a few "famous" curves have equations that are given implicitly. We can use implicit differentiation to find the slope at various points on those curves. We investigate two such curves in the next examples. It is easy to verify that the points , and (0,-1) all lie on the graph.
We can find the slopes of the tangent lines at each of these points using our formula for y′. Note that where functions have vertical tangent lines, they are not differentiable at that point. You now know all of the techniques needed to differentiate a large class of functions.
You should also understand the connection between the derivative, rates of change, and the slope of a tangent line to a curve. In Unit 3the ideas introduced in this unit will be applied to a number of different applications. Implicit differentiation allows us to find slopes of tangents to curves that are clearly not functions . We are using the idea that portions of are functions that satisfy the given equation, but that is not actually a function of .
Find the equations of the horizontal tangent lines. Use a straight edge to verify that the tangent line points straight up and down at that point. Test the point by plugging it into the formula .
If the right-hand side of the equation differs from the left-hand side , then there is a vertical tangent line at that point. We use implicit differentiation to find derivatives of implicitly defined functions . We are using the idea that portions of \(y\) are functions that satisfy the given equation, but that y is not actually a function of \(x\). This result is the equation of the tangent line to the given function at the given point. When we have a function that isn't defined explicitly for ???
Implicit differentiation proves to be useful as it allows us to find the instantaneous rates of change of a variety of functions. We close with a small gallery of "interesting" and "famous" curves along with the implicit equations that produce them. This section has shown how to find the derivatives of implicitly defined functions, whose graphs include a wide variety of interesting and unusual shapes. Implicit differentiation can also be used to further our understanding of "regular" differentiation. Finding the equation of a horizontal tangent to a curve that is defined implicitly as an equation in x and y.
This is the currently selected item. Find a value of x that makes dy/dx infinite; you're looking for an infinite slope, so the vertical tangent of the curve is a vertical line at this value of x. To find the points at which the tangent line is horizontal, we have to find where the slope of the function is 0 because a horizontal line's slope is 0. Now set it equal to 0 and solve for x to find the x values at which the tangent line is horizontal to given function. The formula for obtained above is defined only if . This makes sense because when or and at these points the tangent lines are vertical.
These features, together with the two tangent lines to the circle at points with , are evident in the following plot. Some curves will have more than one vertical tangent. Always make sure you have found all the values of x that make the gradient infinite. You can use graph-plotting software to check by eye for places where the gradient becomes vertical. A tangent of a curve is a line that touches the curve at one point.
It has the same slope as the curve at that point. A vertical tangent touches the curve at a point where the gradient of the curve is infinite and undefined. On a graph, it runs parallel to the y-axis. 2) Plug x value of the indicated point into f ' to find the slope at x.
3) Plug x value into f to find the y coordinate of the tangent point. 4) Combine the slope from step 2 and point from step 3 using the point-slope formula to find the equation for the tangent line. We'll use implicit differentiation, since solving our equation for ???
Is a little tedious and gives us an ugly value. Remember that whenever we take the derivative of a term involving ??? The solutions to the system can be found by using the Solve command to find values for the two variables x and y that make both equations true. Notice that parentheses are used to indicate that z1 is a function of x and y and that the variables to be found, x and y, are enclosed within braces. 28., find the equation of the tangent line to the graph of the implicitly defined function at the indicated points.
As a visual aid, each function is graphed. In this chapter we have defined the derivative, given rules to facilitate its computation, and given the derivatives of a number of standard functions. We restate the most important of these in the following theorem, intended to be a reference for further work. So, why would we want the second derivative? Well, recall from your Calculus I class that with the second derivative we can determine where a curve is concave up and concave down.
We could do the same thing with parametric equations if we wanted to. By using implicit differentiation, we can find the equation of a tangent line to the graph of a curve. We need to know that the derivative is infinite atto have a vertical tangent.
We can see this from the graph, so we have a vertical tangent at. Notice that the derivative is of the form 0/0 at . Implicit functions are generally harder to deal with than explicit functions. With an explicit function, given an x value, we have an explicit formula for computing the corresponding y value.
With an implicit function, one often has to find x and y values at the same time that satisfy the equation. It is much easier to demonstrate that a given point satisfies the equation than to actually find such a point. Basic Derivative Examples - A few examples of finding derivatives for 'easy' functions. This is the set of parametric equations that we used in the first example and so we already have the following computations completed. We'll first need the derivatives of the parametric equations. An expression for obtained by implicit differentiation will typically involve both and .
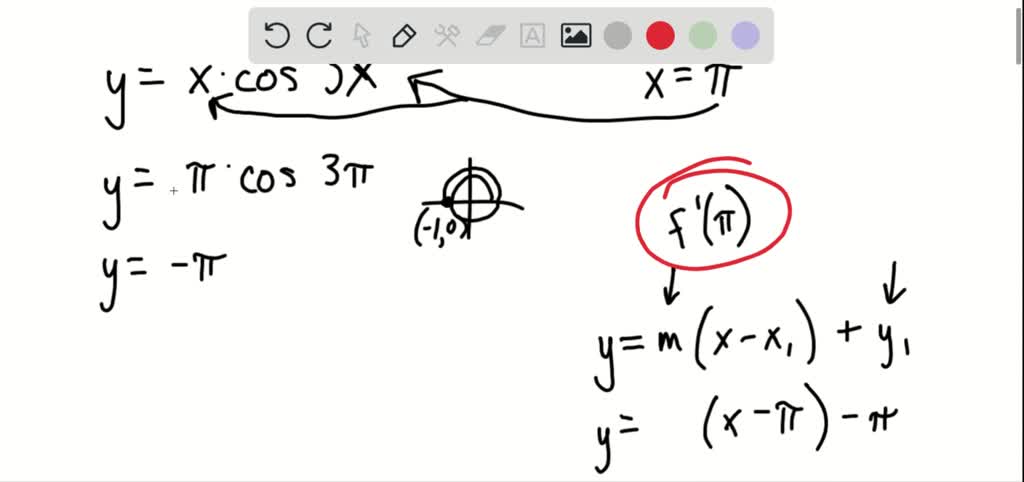
Examples 1 and 2 demonstrate how this form for the derivative can be used effectively. The final example extends the Power Rule from integer to rational exponents. Implicit differentiation will be used in the Related Rateslesson. The equation of the tangent line is .
To determine where the line intersects the -axis, solve . The missile intersects the -axis at the point . Using equation labels, form the sequence of equations consisting of the equation of the Folium and the implicit derivative set equal to 1.
Differentiate implicitly, plug in the point of tangency to find the slope, then put the slope and the tangent point into the point-slope formula. One method to find the slope is to take the derivative of both sides of the equation with respect to x. When taking the derivative of an expression that contains y, you must treat y as a function of x. This method is called implicit differentiation and it is illustrated below. Dydx is the same for each of the following implicitly defined functions. The tangent lines have been added to the graph of the function in Figure 2.6.4.
Notice how our curve looks much different than other functions we have worked with up to this point. Such curves are important in many areas of mathematics, so developing tools to deal with them is also important. Take the derivative of each term in the equation. When taking the derivatives of y terms, the usual rules apply except that, because of the Chain Rule, we need to multiply each term by y′. Find the derivative of the function. The derivative (dy/dx) will give you the gradient of the curve.
Summary of Curve Sketching - Example 2 - Part 2 of 4. In this video, I discuss finding horizontal and vertical asymptotes. Increasing/Decreasing , Local Maximums/Minimums - The basic idea! In this video, I just give a graph and discuss intervals where the function is increasing and decreasing. I also discuss local maximums and minimums.
We know that \[\dfrac\] is the slope of the tangent at any point \[\] on given function. The derivative has many applications in "real life"; one of the most useful is to find the rate of change of one variable with respect to another. Think of a rate of change, or sometimes called an instantaneous rate of change as how fast something is changing at a certain point, like a point in time.
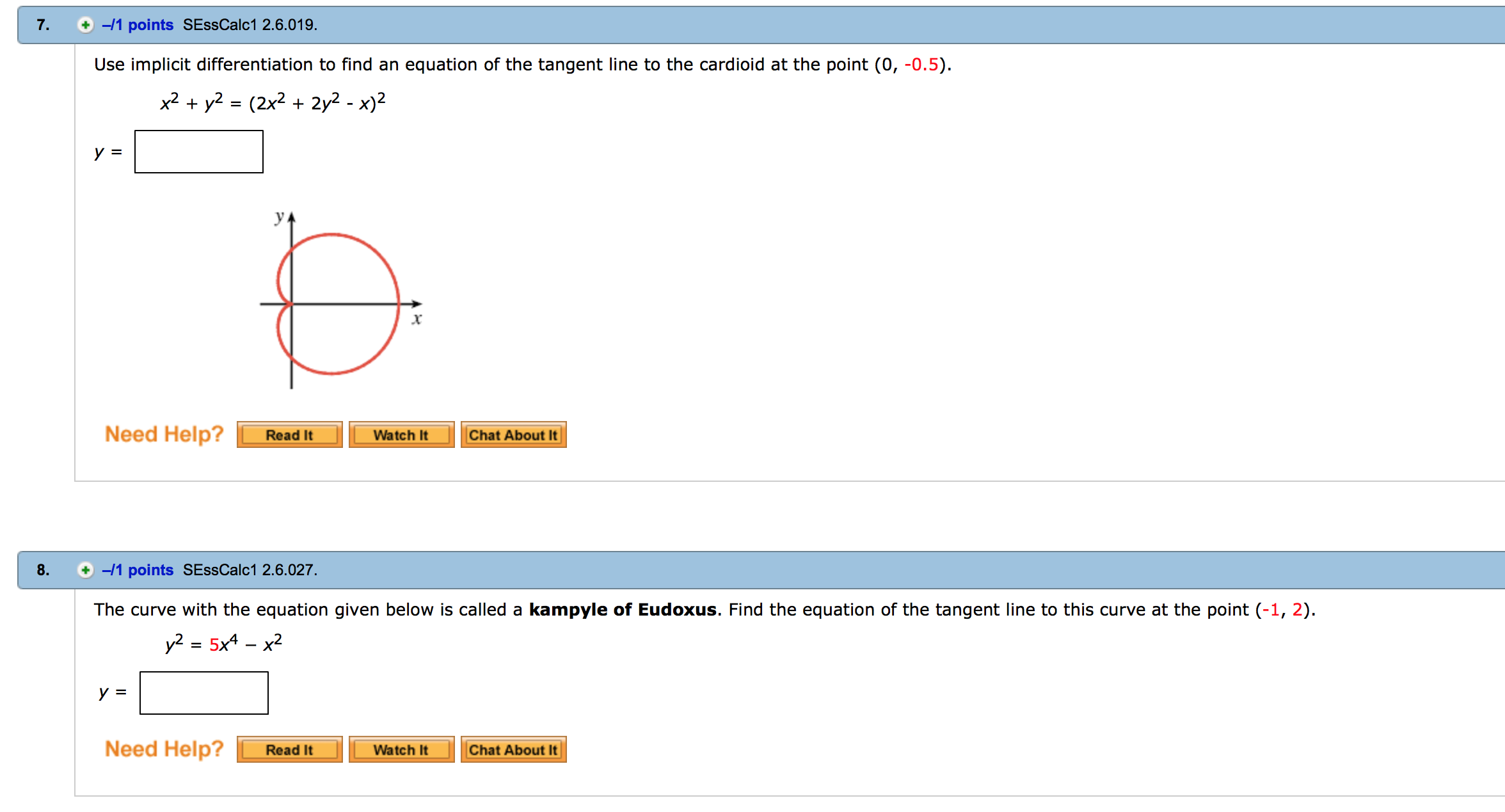
A consequence of the chain rule is the technique of implicit differentiation. Graphing can sometimes help you see where a vertical tangent line might be. Find the equation of the line tangent to the graph of at the point (). This curve is known as the folium of Descartes. Follow the problem solving strategy, remembering to apply the chain rule to differentiate and .
In most discussions of math, if the dependent variable is a function of the independent variable , we express in terms of . If this is the case, we say that is an explicit function of . For example, when we write the equation , we are defining explicitly in terms of . For example, the equation defines the function implicitly. Use implicit differentiation to determine the equation of a tangent line.